So: Gerrymandering.  Everyone agrees that it’s a problem (“just look at that twisty district!”), but it’s hard to agree on a solution.  In particular, I’m learning, it’s tough to define a threshold for gerrymandering in a way that’s useful for a court, judge, or other impartial referee to use.  Getting that impartial referee is super-hard. Giving that referee the tools to use to do their job is, I’m learning, the other half of the challenge.

I’ve been working through the article “Here’s How We Can End Gerrymandering Once and for All“, which is an attempt to come up with a useful, repeatable mathematical threshold for defining an unacceptably gerrymandered district.  That article is a summary of the more formal “Partisan Gerrymandering and the Efficiency Gap“, published in the University of Chicago Law Review.

In the article, Eric McGhee and Nicholas Stephanopoulos calculate an “Efficiency Gap” to measure how out-of-balance a district is.  To calculate the efficiency gap, you start by counting the number of “wasted votes” that each side had in a given election.

Wasted votes come in two flavors:

• “Lost” votes are votes cast for the candidate that is defeated
• “Surplus” votes are votes cast for the winning candidate in excess of the number needed to win.

“The efficiency gap is simply the difference between the parties’ respective wasted votes in an election, divided by the total number of votes cast.”

The authors go into some detail in a hypothetical example, but honestly the textual explanation was clear as mud to me, so I thought I’d work it out on the widely-shared “How to Steal an Election” diagram.  Surely there would be a low efficiency gap in the “fair” example, and a high efficiency gap in the “unfair”, “stolen” example!

Surprisingly, it didn’t work out that way.

Scenario A: Compact and Contiguous

I started by calculating the wasted votes and the efficiency gap for the middle diagram, which is the one I had thought of as “fair.”  In the diagram below, the 50 votes are split into five compact and contiguous districts.  Red is the minority of votes in each district – that’s four “lost” votes for red in each of the districts.  Blue has six votes in each district. That’s exactly the margin needed to win, so there are zero surplus votes:

Twenty total wasted votes for red, zero total wasted votes for blue.  The difference of twenty and zero is twenty.  Twenty divided by fifty total votes is 0.4.  So that’s a 40% efficiency gap in blue’s favor.

Scenario B: Packing and Cracking

Next I turned to the diagram that’s used as an example of gerrymandering.  Eighteen blue voters are “packed” into two districts, and the remaining twelve blue voters are “cracked” into three remaining majority-red districts.  The intention is to give red a majority of representation, even though red has a minority of votes.

In the two packed districts, red has one lost vote and blue has 3 surplus votes. In the three cracked districts, red has zero surplus votes and blue has four lost votes.

That’s a total of two wasted votes for red and eighteen wasted votes for blue.  The difference of eighteen and two is sixteen.  Sixteen divided by fifty total votes is 0.32. So in this diagram, there’s a thirty-two percent efficiency gap in Red’s favor.

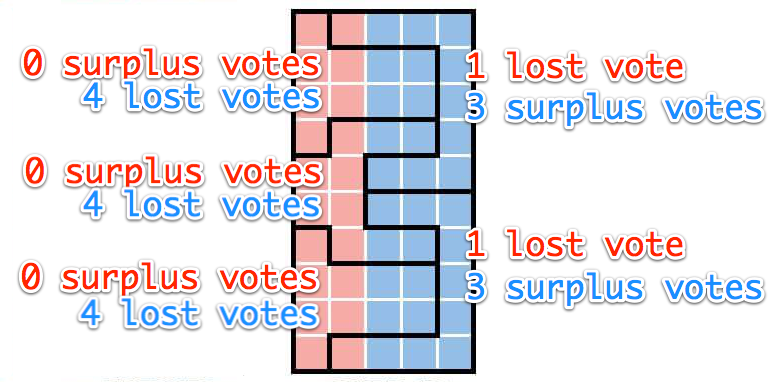
Here’s the thing that I totally did not expect to come out of this exercise: going by the efficiency gap, the “bad” gerrymandered diagram is actually fairer than the “good” contiguous diagram!  

That starts to makes sense if I look at the amount of representation in the example.  Overall, there are sixty blue voters and forty red voters.  In Scenario A, no red voter has a representative.  At all.  If you’re a red voter, you have no representation, period.  In scenario B, red voters have four representatives and blue voters have two representatives.

The majority of representatives is out of balance, but overall, more voters actually have folks that represent them.

I should point out that a 40% efficiency gap and a 32% efficiency gap are both terrible. Kate tells me that the Fair Districts PA folks, using Wisconsin as a benchmark, considers a 7% efficiency gap to be the maximum allowable.  So this example in no way shows that gerrymandering is “good” or anything like that; it just served to teach me that “compact and contiguous” isn’t automatically the same thing as “fair”.

Since electoral maps aren’t actually made up of neat rectangles of voters lined up in ranks and files, I think I’ve exhausted the usefulness of this exercise.  But I think I get the point of the efficiency gap math now — as well as an underlying goal of Fair Districts PA — the point isn’t to get the “right” majority, the point is to minimize the number of “wasted” votes, and maximize the number of voters who get to choose their representative.

A third scenario: what about “perfect” districts?

Okay, I wanted to see what the theoretically completely fair example would be — but even that did not come out the way I expected:

I had thought that districts where the voters were grouped together would have a zero efficiency gap, but I was forgetting about surplus votes.  In the example above, every district has four surplus votes.  The difference between the surplus votes is pretty small — a difference of four votes, which out of fifty total means there’s an 8% efficiency gap in blue’s favor.

Clearly, Scenario C is better than the other two scenarios, since the blue folks get a blue representative, the red folks get a red representative, and the ratio of representatives is commensurate with the ratio of red and blue voters.

BUT! The existence of the “wasted” votes in this scenario, in the form of the four surprus votes in each district, reveals another problem.  The districts are not competitive.  A blue representative doesn’t have to do anything to get elected, assuming their party doesn’t throw a primary challenger at them.  Kate points out that it’s good to have competitive districts, because that encourages moderate candidates that can appeal to as many voters in both groups as possible.  That makes sense to me! But that’s probably a topic for another blog post.

I’d be really interested in your perspective on what I’m overlooking, here.  Is there useful further reading that you’d suggest?